We needed a way to help students with large numbers multiplication. Regular practice with a tool could make things easier. Found out, a multiplication chart up to 100x100 would be handy. Yet, finding a good one ain't simple.
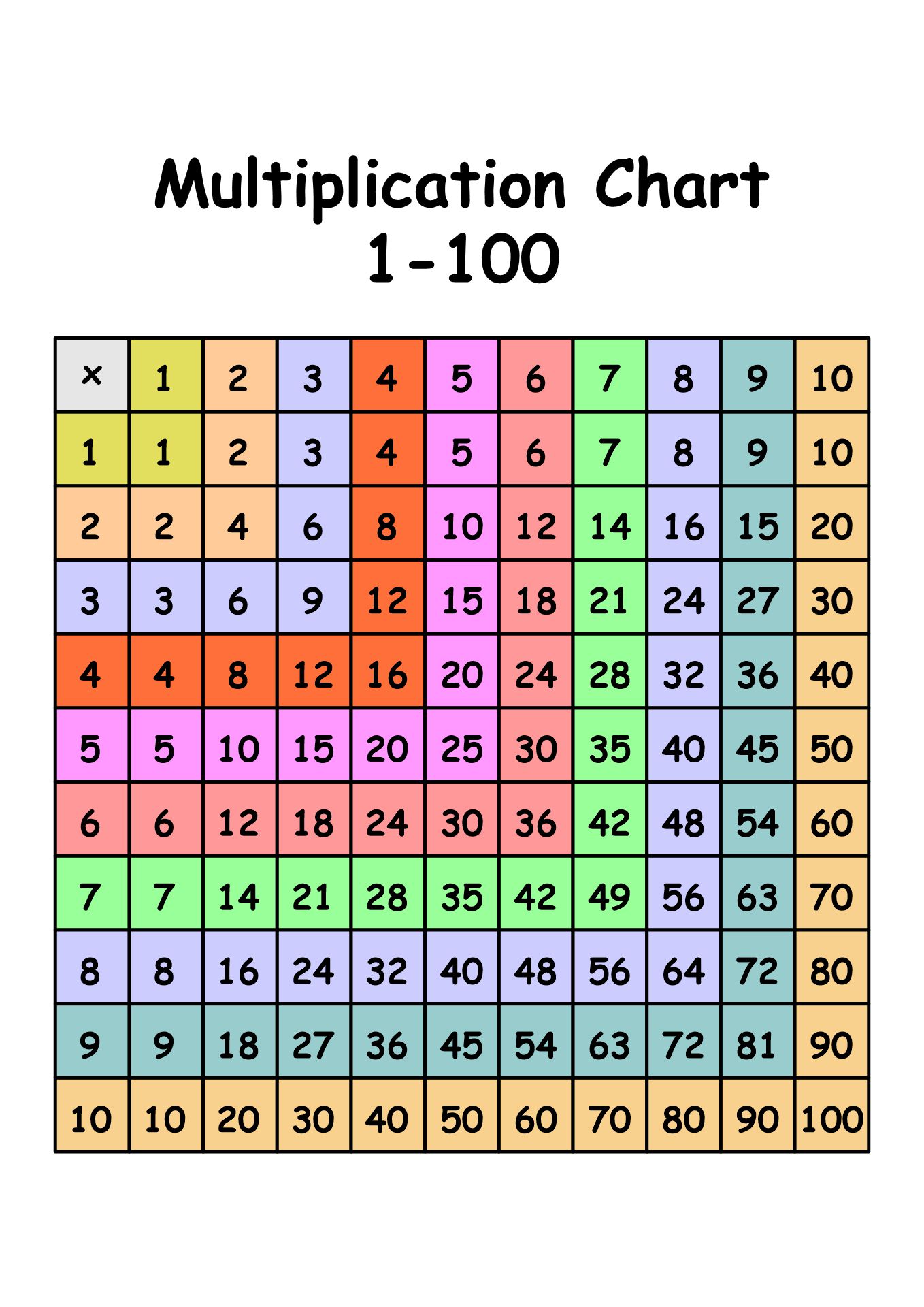
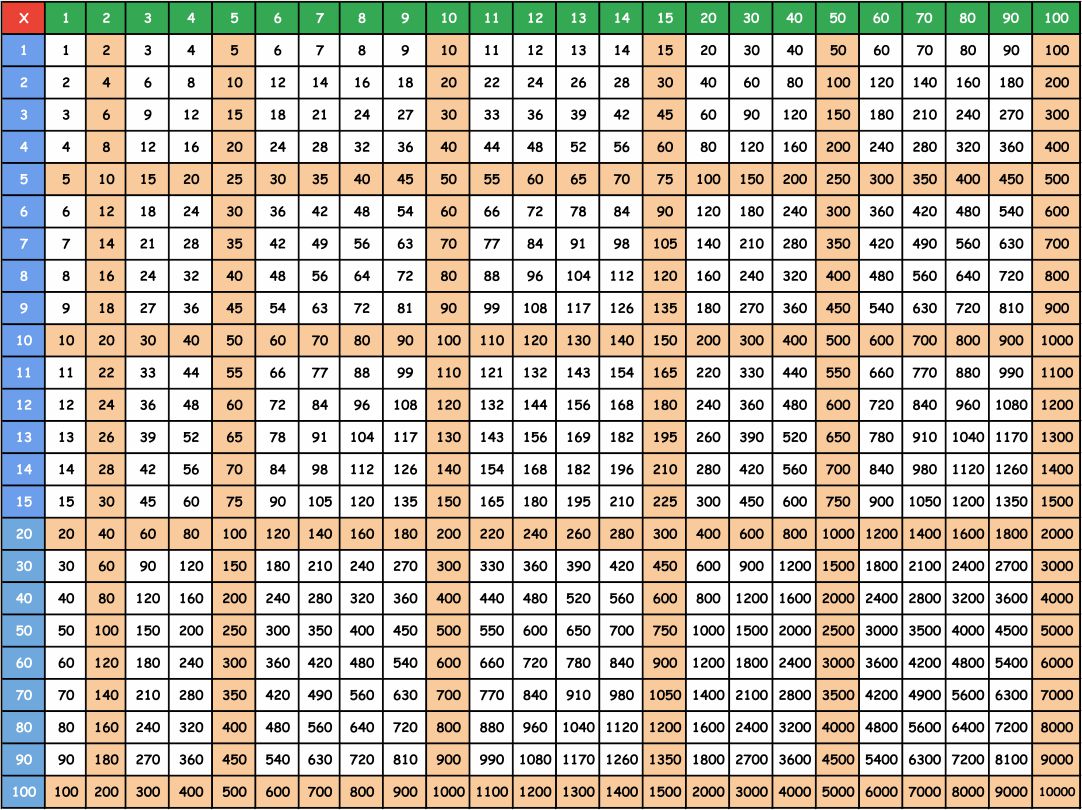
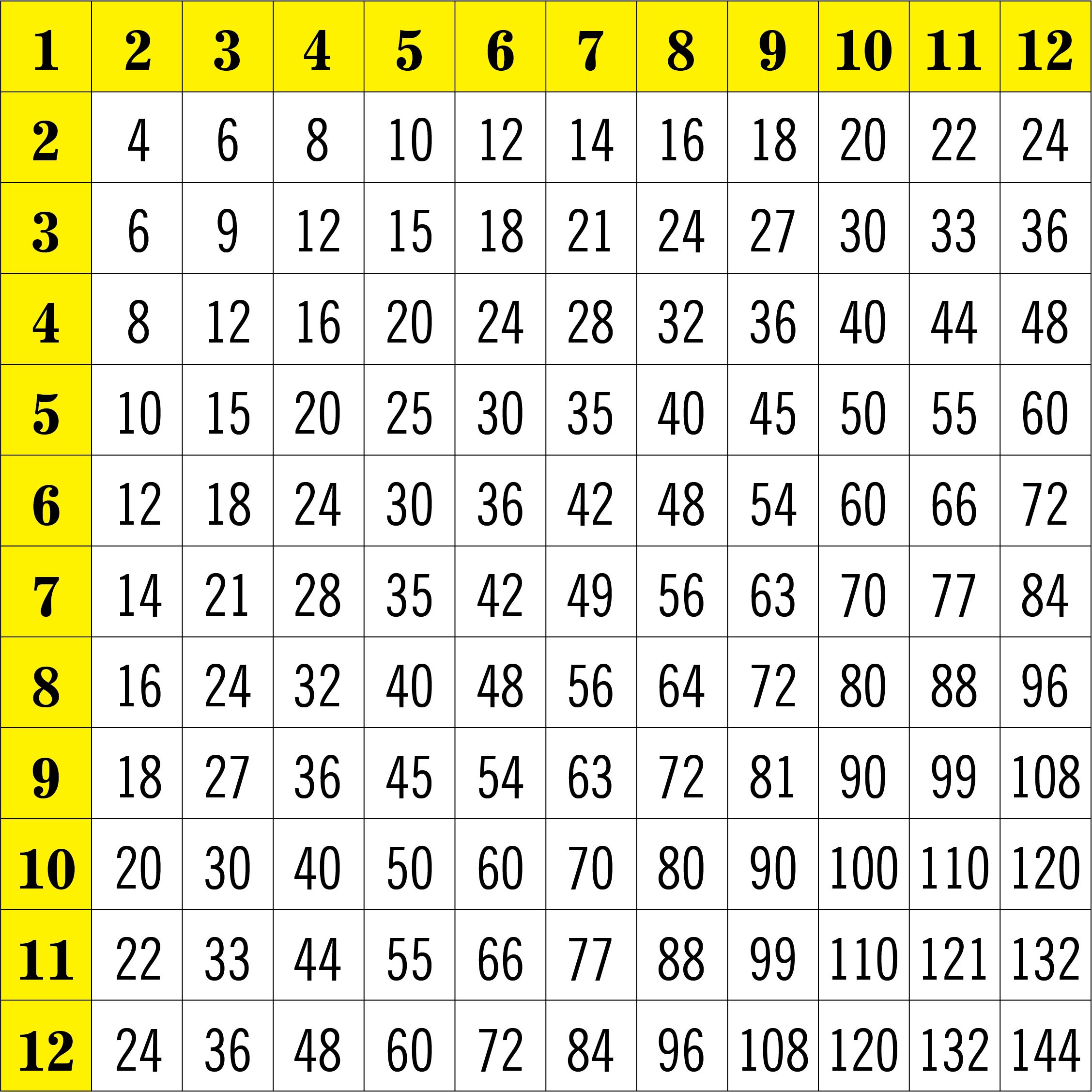
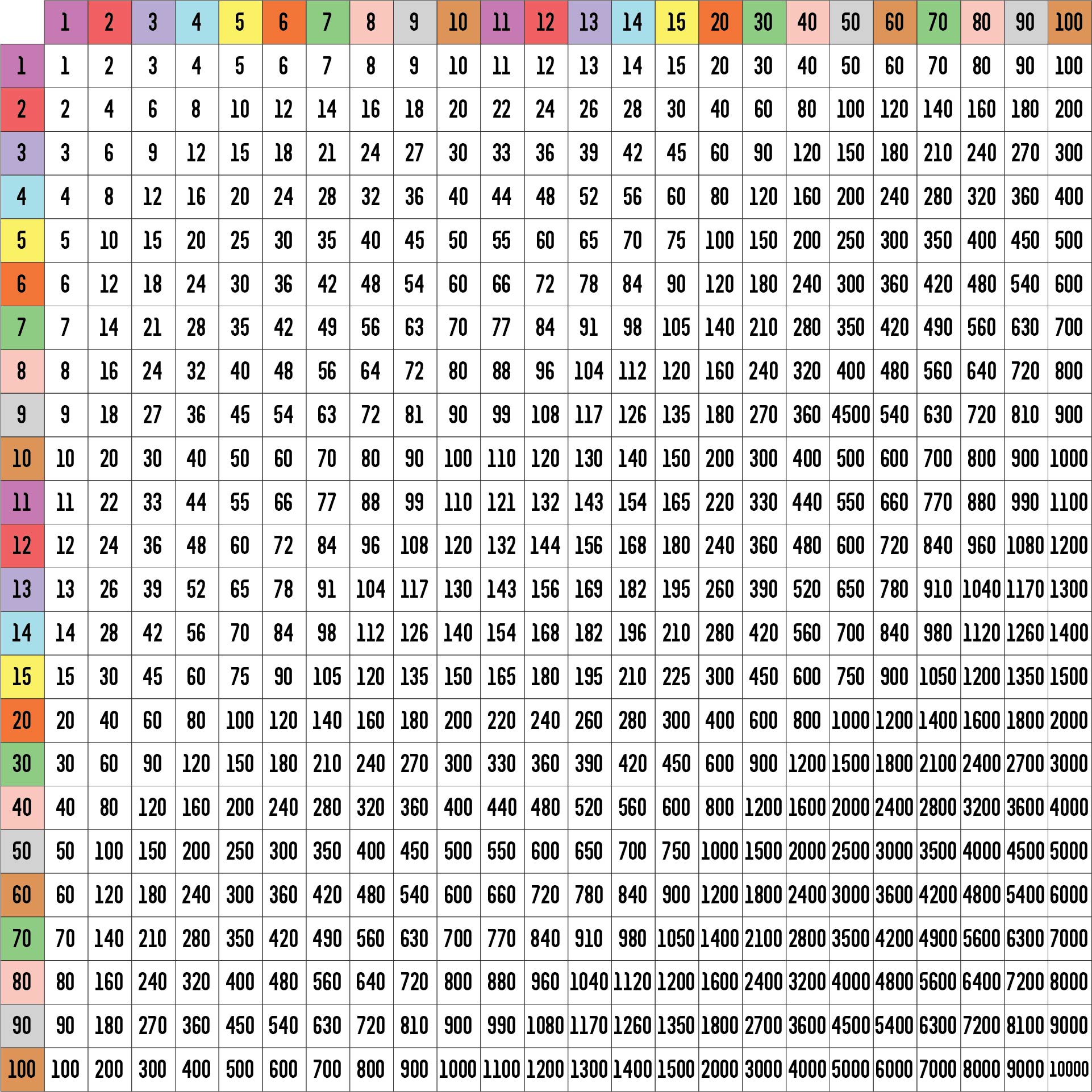
We put together a printable multiplication chart that goes up to 100 x 100. This chart helps with learning and practicing multiplication. Making it visually easy to understand patterns in numbers can boost learning. It's designed to be a go-to resource when practicing multiplication skills.
Printable Multiplication Chart 100 X
Multiplication Chart Up to 100
Multiplication Table Chart Up to 100
Multiplication Table 100X100 Chart
Multiplication Chart 100X100
Multiplication Times Table Chart Up to 100
Multiplication Table Chart Up to 12
Multiplication Chart To 100
Multiplication Chart Of 100
Multiplication Table Of 100
100x100 Multiplication Chart
Our regular activities frequently involve basic mathematical calculations without our even being aware of it. We use mathematical ideas and abilities to grasp time, patterns, and statistics, as well as to calculate cooking measurements, plan travel routes, and budget our money. It supports our ability to solve issues, make wise decisions, and make sense of the world.
Mathematical patterns are closely related to the beauty of nature. Mathematical rules are followed by the hypnotic spirals of seashells, the fractal architectures of ferns, and the symmetry of flower petals. The intricate patterns observed in nature are created by mathematical principles such as Fibonacci sequences, golden ratios, and fractal geometry.
Mathematics is the engine that drives innovation and technology. Data analysis, coding languages, and sophisticated algorithms all have their roots in mathematics. Mathematics offers the basis for discoveries and improvements that form our modern world, from computer graphics to cryptography, from artificial intelligence to medical imaging.
Mathematics has a significant effect on both art and design. Geometric concepts are used by architects to design sturdy and aesthetically pleasing structures. To produce harmonious compositions, artists use mathematical ideas like perspective, symmetry, and proportion. In addition to enhancing aesthetics, mathematics in art allows for exact calculations and rigorous design.
The problem-solving abilities through mathematics go beyond calculating equations. It promotes analytical thinking, critical reasoning, and logical thinking. Mathematical training fosters the capacity to deconstruct difficult issues, spot patterns, and come up with answers. This approach to problem-solving improves our skills in many facets of life, from overcoming obstacles in our daily lives to answering scientific questions.
The multiplication chart as visual aid is useful and could be a resource for learning about and using multiplication. It offers a well-organized breakdown of the results of multiplying numbers, assisting with computations and promoting a deeper comprehension of multiplication ideas.
Multiplication is a critical component of financial planning and computations. A multiplication chart may be a useful tool for doing rapid calculations, whether you're working on interest rates, loan repayments, or investment returns.
Christmas
Have something to tell us?
Recent Comments
This printable multiplication chart is a helpful tool to enhance math skills. It provides a clear and organized layout for practicing multiplication up to 100, making learning enjoyable.
The printable multiplication chart 100 x offers an easy-to-read and convenient tool for children to practice and memorize multiplication facts up to 100, ensuring accurate calculations and fostering numerical fluency.